- This gives the following CRC polynomial (press RETURN to update): P (x) = x8+ x5+ x4+ x0. Enter your message as sequence of hex bytes here. Don't care about whitespaces since they will be ignored. Press RETURN or the Calculate button below to see the CRC checksum here: $ 23.
- Cyclic redundancy check. CRC polynomial: x 32 + x 26 + x 23 + x 22 + x 16 + x 12 + x 11 + x 10 + x 8 + x 7 + x 5 + x 4 + x 2 + x + 1. Used in V.42, MPEG-2. CRC XMODEM: Cyclic redundancy check. CRC polynomial: x 16 + x 12 + x 5 + 1. Custom CRC: Allows you to specify the polynomial values used in checksum calculation.
- Final XOR Value: Enter the value to be XORed with the final value of the CRC algorithm, in hex. For a 16-bit CRC, its low 16 bits will be used; for a 32-bit CRC, the whole 32 bits will be used. Hex Byte CRC: Displays the CRC of your input text (or file) before XORed with Final XOR Value.
- CRC/CCITT (16 bit) 2: 16 bit Cyclic Redundancy Check (CRC) with a polynomial of 0x1021 and an initial value of 0xFFFF. CRC (32 bit) 4: 32 bit Cyclic Redundancy Check (CRC) with a polynomial of 0x04C11DB7 and an initial value of 0xFFFFFFFF. Custom CRC (16 bit) 2: 16 bit Cyclic Redundancy Check (CRC) with a user supplied polynomial and initial value.
However, some checksum algorithms need to treat the data file as a list of unsigned shorts, ints, or int64s (see Using the Inspector for more information on different data types). These type of checksums can be calculated by selecting the Checksum - UShort, Checksum - UInt, or Checksum - UInt64 algorithms respectively.
Hexadecimal Calculation—Add, Subtract, Multiply, or Divide
Convert Hexadecimal Value to Decimal Value
Convert Decimal Value to Hexadecimal Value
The hexadecimal number system (hex) functions virtually identically to the decimal and binary systems. Instead of using a base of 10 or 2 respectively, it uses a base of 16. Hex uses 16 digits including 0-9, just as the decimal system does, but also uses the letters A, B, C, D, E, and F (equivalent to a, b, c, d, e, f) to represent the numbers 10-15. Every hex digit represents 4 binary digits, called nibbles, which makes representing large binary numbers simpler. For example, the binary value of 1010101010 can be represented as 2AA in hex. This helps computers to compress large binary values in a manner that can be easily converted between the two systems.
Below are some typical conversions between hex, binary, and decimal values:
Hex/Decimal Conversion
| Hex | Binary | Decimal |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
| 14 | 10100 | 20 |
| 3F | 111111 | 63 |
Converting between decimal and hex involves understanding the place values of the different number systems. A more in-depth discussion is available on the binary calculator page. Note that converting between decimal and hex is quite similar to converting between decimal and binary. The ability to perform the conversion of either should make the other relatively simple. As previously mentioned, hex functions using the base of 16. This means that for the value 2AA, each place value represents a power of 16. Starting from the right, the first 'A' represents the 'ones' place, or 160. The second 'A' from the right represents 161, and the 2 represents 162. Remember that 'A' in hex is equivalent to 10 in decimal. Knowing this information, it is then possible to convert from hex to decimal, as shown below:
| EX: | 2AA = (2 × 162) + (A × 161) + (A × 160) |
| = (2 × 256) + (10 × 16) + (10 × 1) | |
| = 512 + 160 + 10 = 682 |
Converting from decimal to hex is slightly more involved, but uses the same concepts. Refer to the steps and examples below. It is important to work through the example provided in conjunction with the listed steps in order to understand the process:
- Find the largest power of 16 that is less than or equal to the number to be converted, which will be referred to as X.
- Determine how many times the power of 16 found in Step 1 goes into X, and take note of that number.
- Multiply the number found in Step 2 by the power of 16 and subtract this value from X. This new value will be referred to as Y.
- Note that the number found in Step 2 will be the value written in the place value for the power of 16 that was found. If, for example, the largest power of 16 was found to be 164, and the number in Step 2 was found to be 3, the hex value would have the number 3 in its 164 place value: 3qrst, where qrst represents the 160 through 3 place values.
- Repeat Steps 1-3 using Y as the new starting value. Continue the process until 16 is larger than the remaining value, and assign the remainder to the 160 place value.
- Assign each of the values found in each iteration of Step 2 to its respective place value to determine the hex value.
| EX: | Convert decimal 1500 to hex | |
| (1) | Largest power = 162 = 256 | |
| (2) | 256 × 5 = 1280, so (5 × 162) | |
| (3) | 1500 - 1280 = 220 | |
| (4) | 16 × 13 = 208, so (13 × 161) | |
| (5) | 220 - 208 = 12 | |
| (6) | 16 is larger than 12, so 12 is the value in the 160 place value | |
| (7) | 1500 = (5 × 162) + (13 × 161) + (12 × 160) | |
| (8) | Remember that 10-15 have letter numerals In hex: 13 = D, and 12 = C | |
| (9) | Therefore the hex value of 1500 is: 5DC | |
Converting from hex to decimal utilizes the same principles, but is arguably simpler. Multiply each digit in the hex value by its corresponding place value, and find the sum of each result. The process is the same regardless of whether the hex value contains letter numerals or not.
| EX: | Convert hex 1024 to decimal | |
| (1) | (1 × 163) + (0 × 162) + (2 × 161) + (4 × 160) | |
| (2) | 4096 + 0 + 32 + 4 = 4132 | |
Hex Addition
Hex addition follows the same rules as decimal addition with the only difference being the added numerals A, B, C, D, E, and F. It may be convenient to have the decimal equivalent values of A through F handy when performing hex operations if the values have not yet been committed to memory. Below is an example of hex addition. Work through the example, and refer to the text below it for further details.
EX:| 18 | 1A | B | ||
| + | B | 7 | 8 | |
| = | 1 | 4 | 2 | 3 |
Hex addition involves calculating basic decimal addition while converting between hex and decimal when values larger than 9 (the numerals A through F) are present. In the example above, B + 8 in decimal is 11 + 8 = 19. 19decimal is 13hex, since there is 1 set of 16, with 3 left over. Just like in decimal addition, the 1 carries over to the next column. Hence, the next column works out to be 1 + A (10) + 7 = 18decimal, or 12hex. Carry over the 1 to the final column resulting in 1 + 8 + B (11) = 20decimal, or 14hex. This yields the result of 1423hex.
Hex File Crc 16 Calculadora Gratis
Hex Subtraction
Hex subtraction can be computed much the same way as hex addition; by performing the operation while converting between hex and decimal values. The most significant difference between hex and decimal subtraction involves borrowing. When borrowing in hex, the '1' that is borrowed represents 16decimal rather than 10decimal. This is because the column that is being borrowed from is 16 times larger than the borrowing column (the same reason that the borrowed 1 in decimal represents 10). As long as this is noted, and conversions of the letter numerals A-F are done carefully, hex subtraction is not any more difficult than decimal subtraction. Work through the example, and refer to the text below it for further details.
EX:| 5 | D | 1C | |
| – | 3 | A | F |
| = | 2 | 2 | D |
In the first column on the right of the above example, C, or 12decimal, is smaller than F, or 15decimal. As such, it is necessary to borrow from the next column. This reduces the D, to C, and lends 1, or 16decimal to the first column. 16decimal + 12decimal - 15decimal = 13decimal, or D in the first column. The following columns require no borrowing, making the calculations simple. Since 1 was borrowed, C - A = 12decimal - 10decimal = 2, and 5 - 3 = 2 yielding the final result of 22D. In the case where the number being subtracted is larger than the number being subtracted from, simply change the positions of the numbers, calculate the subtraction, and add a negative sign to the result. If the above example were instead 3AF - 5DC, it would then be written as is, except that the solution would be -22D.
Hex Multiplication
Hex multiplication can be tricky because the conversions between hex and decimal when performing the operations require more effort since the numerals tend to be larger. Having a hexadecimal multiplication table can be helpful (one is provided below). Otherwise, manual conversion between decimal and hex will be necessary for each step. Below is an example of hex multiplication. To the right of the example, each of the multiplication and addition steps is shown. Note that all of the numerals used are hex. Refer to the addition section if necessary.
EX:| F | A | 3 × A = 1E; 1 carried to F | |||
| × | C | 3 | 3 × F = 2D, + 1 = 2E | ||
| 2 | E | E | C × A = 78; 7 carried to F | ||
| + | B | B | 8 | 0 | C × F = B4, + 7 = BB |
| = | B | E | 6 | E |
Hex Division
Long division in hex is identical to long division in decimal, except that the multiplication and subtraction occur in hex. It is also possible to convert to decimal and perform long division in decimal, then convert back once complete. For illustrative purposes, the division example will be calculated entirely in hex. As with multiplication, having a hexadecimal multiplication table (one is provided below) would be convenient while conducting hex division. Below is an example. Note that all numerals in the example are hex. Although no borrowing occurs in the example below, remember that borrowing in hex results in 16decimal being borrowed, rather than 10decimal. Refer to the hex subtraction section for further details.
Hexadecimal Multiplication Table
Hex File Crc Calculator
Introduction on CRC calculations
Whenever digital data is stored or interfaced, data corruption might occur. Since the beginning of computer science, people have been thinking of ways to deal with this type of problem. For serial data they came up with the solution to attach a parity bit to each sent byte. This simple detection mechanism works if an odd number of bits in a byte changes, but an even number of false bits in one byte will not be detected by the parity check. To overcome this problem people have searched for mathematical sound mechanisms to detect multiple false bits. The CRC calculation or cyclic redundancy check was the result of this. Nowadays CRC calculations are used in all types of communications. All packets sent over a network connection are checked with a CRC. Also each data block on your hard-disk has a CRC value attached to it. Modern computer world cannot do without these CRC calculation. So let’s see why they are so widely used. The answer is simple, they are powerful, detect many types of errors and are extremely fast to calculate especially when dedicated hardware chips are used.
One might think, that using a checksum can replace proper CRC calculations. It is certainly easier to calculate a checksum, but checksums do not find all errors. Lets take an example string and calculate a one byte checksum. The example string is “Lammert” which converts to the ASCII values [ 76, 97, 109, 109, 101, 114, 116 ]. The one byte checksum of this array can be calculated by adding all values, than dividing it by 256 and keeping the remainder. The resulting checksum is 210. You can use the calculator above to check this result.
In this example we have used a one byte long checksum which gives us 256 different values. Using a two byte checksum will result in 65,536 possible different checksum values and when a four byte value is used there are more than four billion possible values. We might conclude that with a four byte checksum the chance that we accidentally do not detect an error is less than 1 to 4 billion. Seems rather good, but this is only theory. In practice, bits do not change purely random during communications. They often fail in bursts, or due to electrical spikes. Let us assume that in our example array the lowest significant bit of the character ‘L‘ is set, and the lowest significant bit of character ‘a‘ is lost during communication. The receiver will than see the array [ 77, 96, 109, 109, 101, 114, 116 ] representing the string “M`mmert“. The checksum for this new string is still 210, but the result is obviously wrong, only after two bits changed. Even if we had used a four byte long checksum we would not have detected this transmission error. So calculating a checksum may be a simple method for detecting errors, but doesn’t give much more protection than the parity bit, independent of the length of the checksum.
The idea behind a check value calculation is simple. Use a function F(bval,cval) that inputs one data byte and a check value and outputs a recalculated check value. In fact checksum calculations as described above can be defined in this way. Our one byte checksum example could have been calculated with the following function (in C language) that we call repeatedly for each byte in the input string. The initial value for cval is 0.
The idea behind CRC calculation is to look at the data as one large binary number. This number is divided by a certain value and the remainder of the calculation is called the CRC. Dividing in the CRC calculation at first looks to cost a lot of computing power, but it can be performed very quickly if we use a method similar to the one learned at school. We will as an example calculate the remainder for the character ‘m‘—which is 1101101 in binary notation—by dividing it by 19 or 10011. Please note that 19 is an odd number. This is necessary as we will see further on. Please refer to your schoolbooks as the binary calculation method here is not very different from the decimal method you learned when you were young. It might only look a little bit strange. Also notations differ between countries, but the method is similar.
With decimal calculations you can quickly check that 109 divided by 19 gives a quotient of 5 with 14 as the remainder. But what we also see in the scheme is that every bit extra to check only costs one binary comparison and in 50% of the cases one binary subtraction. You can easily increase the number of bits of the test data string—for example to 56 bits if we use our example value “Lammert“—and the result can be calculated with 56 binary comparisons and an average of 28 binary subtractions. This can be implemented in hardware directly with only very few transistors involved. Also software algorithms can be very efficient.
For CRC calculations, no normal subtraction is used, but all calculations are done modulo 2. In that situation you ignore carry bits and in effect the subtraction will be equal to an exclusive or operation. This looks strange, the resulting remainder has a different value, but from an algebraic point of view the functionality is equal. A discussion of this would need university level knowledge of algebraic field theory and I guess most of the readers are not interested in this. Please look at the end of this document for books that discuss this in detail.
Now we have a CRC calculation method which is implementable in both hardware and software and also has a more random feeling than calculating an ordinary checksum. But how will it perform in practice when one ore more bits are wrong? If we choose the divisor—19 in our example—to be an odd number, you don’t need high level mathematics to see that every single bit error will be detected. This is because every single bit error will let the dividend change with a power of 2. If for example bit n changes from 0 to 1, the value of the dividend will increase with 2n. If on the other hand bit n changes from 1 to 0, the value of the dividend will decrease with 2n. Because you can’t divide any power of two by an odd number, the remainder of the CRC calculation will change and the error will not go unnoticed.

The second situation we want to detect is when two single bits change in the data. This requires some mathematics which can be read in Tanenbaum’s book mentioned below. You need to select your divisor very carefully to be sure that independent of the distance between the two wrong bits you will always detect them. It is known, that the commonly used values 0x8005 and 0x1021 of the CRC16 and CRC-CCITT calculations perform very good at this issue. Please note that other values might or might not, and you cannot easily calculate which divisor value is appropriate for detecting two bit errors and which isn’t. Rely on extensive mathematical research on this issue done some decades ago by highly skilled mathematicians and use the values these people obtained.
Furthermore, with our CRC calculation we want to detect all errors where an odd number of bit changes. This can be achieved by using a divisor with an even number of bits set. Using modulo 2 mathematics you can show that all errors with an odd number of bits are detected. As I have said before, in modulo 2 mathematics the subtraction function is replaced by the exclusive or. There are four possible XOR operations.
We see that for all combinations of bit values, the oddness of the expression remains the same. When choosing a divisor with an even number of bits set, the oddness of the remainder is equal to the oddness of the dividend. Therefore, if the oddness of the dividend changes because an odd number of bits changes, the remainder will also change. So all errors which change an odd number of bits will be detected by a CRC calculation which is performed with such a divisor. You might have seen that the commonly used divisor values 0x8005 and 0x1021 actually have an odd number of bits, and not even as stated here. This is because inside the algorithm there is a “hidden” extra bit 216 which makes the actual used divisor value 0x18005 and 0x11021 inside the algorithm.
Last but not least we want to detect all burst errors with our CRC calculation with a maximum length to be detected, and all longer burst errors to be detected with a high probability. A burst error is quite common in communications. It is the type of error that occurs because of lightning, relay switching, etc. where during a small period all bits are set to one. To really understand this you also need to have some knowledge of modulo 2 algebra, so please accept that with a 16 bit divisor you will be able to detect all bursts with a maximum length of 16 bits, and all longer bursts with at least 99.997% certainty.
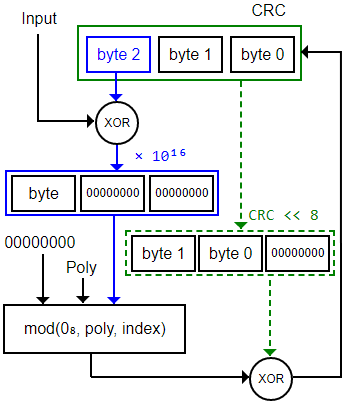
In a pure mathematical approach, CRC calculation is written down as polynomial calculations. The divisor value is most often not described as a binary number, but a polynomial of certain order. In normal life some polynomials are used more often than others. The three used in the on-line CRC calculation on this page are the 16 bit wide CRC16 and CRC-CCITT and the 32 bits wide CRC32. The latter is probably most used now, because among others it is the CRC generator for all network traffic verification and validation.
For all three types of CRC calculations I have a free software library available. The test program can be used directly to test files or strings. You can also look at the source codes and integrate these CRC routines in your own program. Please be aware of the initialization values of the CRC calculation and possible necessary post-processing like flipping bits. If you don’t do this you might get different results than other CRC implementations. All this pre and post-processing is done in the example program so it should be not to difficult to make your own implementation working. A common used test is to calculate the CRC value for the ASCII string “123456789”. If the outcome of your routine matches the outcome of the test program or the outcome on this website, your implementation is working and compatible with most other implementations.
Just as a reference the polynomial functions for the most common CRC calculations. Please remember that the highest order term of the polynomial (x16 or x32) is not present in the binary number representation, but implied by the algorithm itself.
Hex File Crc 16 Calculadora En
Truth is what stands the test of experience. |